
コンテンツ
しばらく前に、私の友人が私がZipfの法則、Paretoの原理、そして彼らの不思議な外見についてVsaucesのビデオを見ることを勧めました。ここにあなたの注意を引くためのちょっとしたティーザーがあります - 全人口の80%が最も人気のある都市の20%に住んでいます。全土地の80%が最も富裕な家主の20%に属します。 Zipfの法則とParetosの原則によると、ゴミの80%がゴミの多い路上の20%にあります。
十分ではない?さて、昨日発見したように、うさぎの穴はそこで止まりません…懐疑論に満ちて、私は人々がどのくらいの時間スチームゲームをするのに費やすか調べることにしました…さて。人の時間の80%が最も人気のあるゲームの20%を遊んでいます...面白いですか?さて、読んでください、この話にはもっとあります。
Vsauces endeavourは、20分以上の時間をかけて、Zipfについての大まかな全体像を説明していますが、Zipfがそれをどのように機能させるのかに貢献すると広く考えられているコアメカニズムを示しています。それで私達が行く前に私はそれを簡単に説明したいと思います。
ジップの法則
20/80原則の背後にある直感を説明するためのいくつかの概念的な方法があります。私の考えでは、最も良い例は月のクレーターに関するものです。
基礎実験
それで、あなたがそうするならば、手つかずの月 - 完全に滑らかな表面 - があると想像してください。さて、月を襲うようなランダムな大きさの小惑星がいくつかあるとしましょう。最初の小惑星が着陸すると、それはクレーターを残します。今度は別の人が当たり、他の場所にクレーターを残します。各クレーターは全表面積の一部なので、次のランダムな小惑星が既存のクレーターの近くに当たってそれと結合し、グループを形成する可能性があります。新しい小惑星が特定のクレーターに当たる可能性は、クレーターと既存の小惑星のサイズに比例します。これは、次のランダム小惑星が最も大きい既存のグループに加わる可能性が高く、それがさらに大きくなることを意味します。一種の累積プロセスで、これにより、金持ち、金持ち、貧乏人というメカニズムが生まれます。
これが覚えておいてください、なぜならそれが「なぜ」のジップの法則がそのような神秘的な普遍性と共に働くかについての一般的な説明であると信じられているからです。小惑星の例は非常に単純ですが、問題は多くの繰り返しで何が起こるのかということです。
ちょっと当惑する?
さて、私はこの最初のポイントを家に帰るためにgifを作りました。 NB!グラフについては後で説明しますが、実験を試してみてください。

実際の月を観察すると、小惑星の量が大量に増加するにつれて、観察されるクレーター直径は最大のクレーターのトップ20%が全表面積の80%に近づくように大きくなります。
それで、私たちがより多くの小惑星に行くにつれて、最も人気のあるグループから最も人気のないグループへの分布は、この20/80の性質を持つある種の「理想的な分布」 - パレート分布に近づきます。あなたが数学をするならば、それは(一般的に)、最大のグループがサイズNを持つならば、2番目に大きいグループはおよそサイズN / 2、3番目のN / 3などとなります。これはジップの法則と呼ばれます。奇妙なことはZipfの法則であり、Pareto分布は当惑する量の要素(小惑星)とグループ(クレータークラスター)に対して機能します。もちろん、ゆがみやランダムな乱れがありますが、一般的な傾向は否定できないです。
すでにたくさんの人が住んでいるのであれば、小惑星が月面の大きなクレーターにぶつかる可能性が高いことが、より魅力的な都市につながっていることがわかるでしょう。しかし、都市はZipfに従って行動する唯一の「グループ」からは程遠いということを理解しなければなりません。
これは、Mark NewmansによるPareto分布の研究の例です。 NB!グラフは対数 - 対数スケールであり、曲線の双曲線形式を滑らかにし、ほぼ線形の関係を示しています。
初期値y = aX ^( - b)
両側のログ=>ログy =ログa - bログX
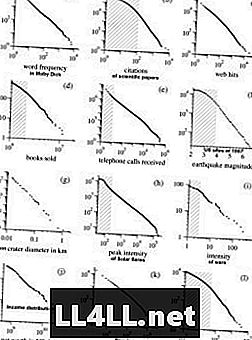
興味深いことに、同じ傾向が宗教的カルトによっても示されています。これらの現象の大部分の共通の性質は、単にこの「大集団が大きくなる」傾向です。そのため、Zipfの法則は、要素の優先順位がグループのサイズに確実に関連している(つまり、グループが大きいほど、グループが大きくなる可能性が高い)メカニズムでは持続的です。これが、私がグループをクラスターとして、そして要素をクラスターとして考えることを好む理由です。
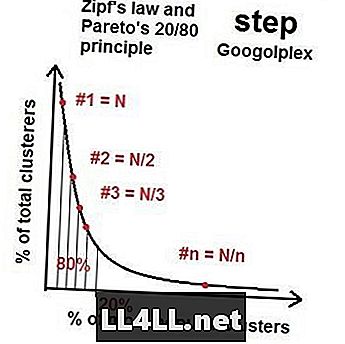
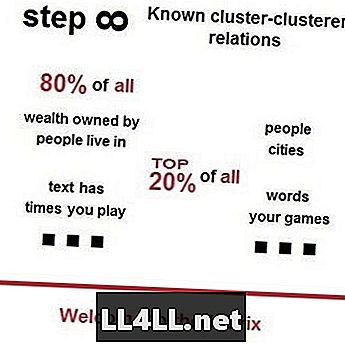
蒸気市場におけるジップの法則
その最後のものの疑い?これは、Steamで最も人気のあるゲームに人々が費やす時間です。SteamSpyからのデータ。
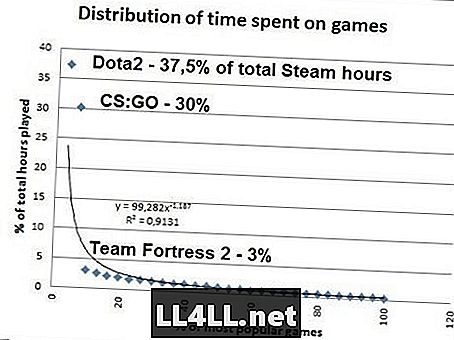
あなたが数学をするならば、それは最も一般的なSteamゲームの20%がプレーの総量の80%を占めるということがわかります、それでPareto 20/80ミステリーはここで魅力のように働きます...しかし、それはジッパーは真実である、 CS:GO なんと30%ではなく、37.5%/ 2 = 18,8%を占める必要があります。しかし、この異常値とは別に(再生を停止します CS:GO)、Zipf風のディストリビューションは明らかにそこにあります。
これは最も人気のあるゲームのために販売されたコピーの量です。
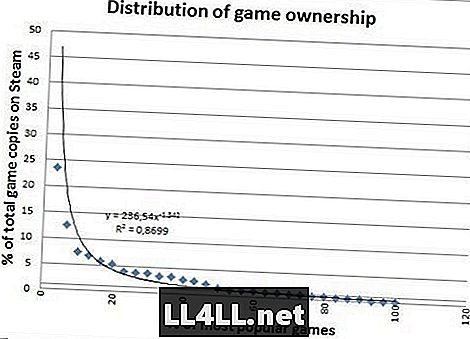
もっと素敵に見える?売られたコピーは大きな異常値を持っていないのでそれは非常によく合います、それは注目に値する違いです。しかし、最後の2つのグラフの違いから結論を出すためにもっと興味深いことがあります。
2番目のグラフでは、右に行く「尾」が太っているのがわかりますか。簡単に言えば、これは「比較的人気のない」ゲームが実際には前のプロットよりもかなり人気があることを示しています。
実際、最も人気のあるゲームの20%が、売り上げの60%にすぎないのに対して、プレーの80%が占めています。面白い?お尻は間違いないでしょう。
私たちはSteamについて何を学ぶことができますか?
さて、ゲームの人気がパレート分布に従うという事実は、確かにある種の積極的なネットワーク効果があり、それによってプレイヤーがすでにより多くの人々によってプレイされているゲームを選択することを意味します。尾の太さの違いが私たちに言うのは、Steamユーザーはゲームを購入するときよりも、ゲームを購入するときの方がはるかに「グループサイズの盲目」だということです。
考えてみましょう。「現在の一般的な意見」に関係なく、より多くの人がゲームを購入するほど、大規模ゲームがさらに成長する可能性は低いため、Paretoディストリビューションはより平坦化されます。誰もがすでにゲームをプレイしていて、すべてのゲームの可用性が同じであることをねばねば言っていないのであれば、最も人気のあるゲームの20%が売り上げとプレイ時間の約50%を占めると予想します。正規分布)
結論
ですから、Steam市場でのParetoディストリビューションに貢献する2つの要因があります - 開発者がどれほど革新的であるか(いくつの新しい月のクレーターが形成されているか) 。結局のところ、ゲーマーはゲームを購入するときは非常にグループ規模の盲目ですが、ゲームをするときはその逆です。クールでしょ?
Zipfの法則とべき乗則の分布についてもっと知りたい場合は、ここがいい講義です。さらに、必ずNewmanの論文を見てください。
この種のものをもっと読みたいのであれば、間もなくこの観察をモデルに参加させようとします。これは、より人気のあるマルチプレイヤーゲームの価格が高いことを示しています。こちらの記事を参照してください。 Piece De Resistanceの記事では、これらの理論を組み合わせて、マルチプレイヤーゲーム、ソーシャルネットワーク、および都市が実際にネットワーク効果を持つすべての反ライバル商品であることを説明しています。このZipfianのミステリーミストで彼らに権利を与えてください...
それまでは、楽しんでください。
P.Sあなたは本当かもしれないと思う20/80関係のための楽しいアイデアでコメントをポップしなさい。
私のものは:
人々の80%のノスタルジアは彼らの最も幸せな記憶の20%が原因で引き起こされています(実際には人々が情報を忘れる率で証明されています)
質量の80%が最大の宇宙物体の20%に集中しています(実際には重力の分布が証明されています)
そしてもちろん
あなたのトイレの混乱の80%はあなたが食べるものの20%から来ています(話す学術研究はありません)